Consejo 1: Cómo convertir números a notación binaria
Consejo 1: Cómo convertir números a notación binaria
Además del sistema decimal habitual cálculo, hay otros sistemas. Los más comunes son binarios, octales, hexadecimales. Estos sistemas se usan principalmente en tecnología informática. Para traducir números de un sistema cálculo en el otro hay operaciones simples. Considera cómo traducir número de en binario el sistema cálculo de otros sistemas.

Instrucciones
1
Traducción octal número de en binario el sistema Es necesario presentar cada una de sus figuras en la formatríada de dígitos binarios. Por ejemplo, el número octal 765 se descompone en tríadas de la siguiente manera: 7 = 111, 6 = 110, 5 = 101. El resultado es un número binario de 111110101.
2
Para traducir el hexadecimal número de en binario el sistema cálculo Es necesario presentar cada una de sus figuras en la formatétradas de dígitos binarios. Por ejemplo, el número hexadecimal 967 se descompone en tétradas de la siguiente manera: 9 = 1001, 6 = 0110, 7 = 0111. El resultado es un número binario de 100101100111.
3
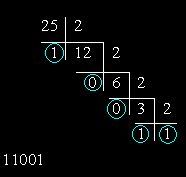
Para convertir el número decimal en binario el sistema cálculo, es necesario dividirlo consistentemente en dos, cada vez que escriba el resultado como un todo número de y el resto. La división debe continuar hasta que haya un número igual a uno. El número final se obtiene al registrar secuencialmente el resultado de la última división y los restos de todas las divisiones en el orden inverso. Como ejemplo, la figura muestra el procedimiento para traducir el decimal número de 25 a binario el sistema cálculo. La división consecutiva en dos da la siguiente secuencia de residuos: 10011. Expandiéndolo, por el contrario, obtenemos el número requerido.
Consejo 2: Cómo convertir a binario
Los componentes de las máquinas electrónicas, a los cualestambién hay computadoras, solo hay dos estados distinguibles: hay una corriente y no hay corriente. Se designan "1" y "0" respectivamente. Como solo hay dos estados, muchos procesos y operaciones en electrónica pueden describirse utilizando números binarios.

Instrucciones
1
Para traducir un decimal fraccionarionúmero en el sistema de números binarios, siga el siguiente algoritmo. Considere la operación del algoritmo usando el ejemplo del número 235.62. En primer lugar, se traduce la parte entera del número.
2
Divida el número decimal por dos hastaobtenemos un residuo indivisible. En cada paso de división, obtenemos el resto 1 (si el número de dividendo es impar) o 0 (si el dividendo es divisible por dos sin residuo). Todos estos residuos deben tenerse en cuenta. El último resultado parcial, obtenido como resultado de dicha división de pasos, siempre será una unidad. Escribimos la última unidad en el dígito más alto del número binario requerido, y los residuos obtenidos en el proceso se anotan para esta unidad en el orden inverso. Aquí debe tener cuidado y no omitir los ceros. Por lo tanto, el número de 235 en el código binario corresponderá al número 11101011.

3
Ahora traduce al sistema numérico binariola parte fraccional del número decimal. Para hacer esto, multiplicamos la parte fraccional del número por 2 y reparamos las partes enteras de los números obtenidos. Estas partes enteras se agregan al número obtenido en el paso anterior después del punto binario en el orden directo. Luego, el número decimal decimal 235.62 corresponde al fraccionario binario 11101011.100111.

Consejo 3: Cómo traducir el sistema numérico
En la tecnología de la información, en lugar del sistema de número decimal habitual, a menudo se utiliza el binario, ya que el trabajo de las computadoras se basa en él.

Instrucciones
1
Las operaciones principales son solo dos: traducción de decimal a otro (binario, octal, etc.) y viceversa. El nombre de cada sistema numérico proviene de su base: el número de elementos en él (binario - 2, decimal - 10). En los sistemas de notación de base con una base mayor a 10, es costumbre usar las letras del alfabeto latino (A-10, B-11, etc.) como reemplazo de números de dos dígitos.
2
Consideremos las operaciones usando el ejemplo de un sistema binarionumeración, como la más común. Para todos los demás sistemas, las mismas reglas y métodos se aplicarán a la sustitución de la base 2 por la correspondiente. Por lo tanto, tenemos un número en el sistema de números binarios, que consta de varios dígitos. Lo escribimos en forma de la suma de los productos de sus dígitos multiplicados por 2. A continuación, organizamos todos los poderes de derecha a izquierda comenzando desde 0. Resumimos. El número resultante es el que está buscando. Ejemplo: 1011 = 2 * 2 + 11.
3
Ahora considere la operación inversa.Deje que se le dé un número en el sistema decimal. Lo dividiremos por una columna en función del sistema numérico en el que queremos traducirlo (en nuestro caso será 2). La división continúa hasta el final, hasta que lo privado se vuelve menos que el suelo. A continuación, comenzando con el último, anotamos todos los restos en la línea. Este es el número requerido. Ejemplo 11/2 = 5 el resto es 1, 5/2 = 2, el resto es 1, 2/2 = 1 el resto es 0 => 1011. Otro ejemplo se muestra en la imagen. Para otras bases, las operaciones son similares. ¡No olvide reemplazar los números, comenzando con 10, en los sistemas numéricos correspondientes en letras latinas! De lo contrario, el número resultante se leerá incorrectamente, porque "10" y "1" "0" son completamente diferentes. La base del sistema numérico, en la que se representa el número, se indica en forma de índice en la parte inferior del dígito más a la derecha del número.

Consejo 4: Cómo traducir números de un sistema a otro
En el sistema de cuenta que usamos cadadía, diez figuras - de cero a nueve. Por lo tanto, se llama decimal. Sin embargo, en cálculos técnicos, especialmente aquellos relacionados con computadoras, otros sistemas, en particular, binario y hexadecimal. Entonces necesitas poder traducir número de de uno sistemas Numeración en otro.

Necesitarás
- - un pedazo de papel;
- - un lápiz o un bolígrafo;
- - calculadora.
Instrucciones
1
El sistema binario es el más simple. Solo tiene dos dígitos, cero y uno. Cada dígito de binario número de, comenzando con el final, corresponde al poder de dos. Dos a cero grados es igual a uno, en el primero - dos, en el segundo - cuatro, en el tercero - ocho, y así sucesivamente.
2
Supongamos que le dan un número binario de 1010110. Las unidades que se encuentran en el segundo, tercero, quinto y séptimo desde el final del campo. Por lo tanto, en el sistema decimal este número es igual a 2 ^ 1 + 2 ^ 2 + 2 ^ 4 + 2 ^ 6 = 2 + 4 + 16 + 64 = 86.
3
El problema inverso es la traducción del decimal número de en el sistema binario Supongamos que tiene un número de 57. Para obtener su registro binario, debe dividir secuencialmente este número entre 2 y escribir el resto de la división. El primer paso le dará el último dígito: 57/2 = 28 (saldo 1). Luego obtendrá el segundo del final: 28/2 = 14 (resto 0). Los siguientes pasos son: 14/2 = 7 (resto 0), 7/2 = 3 (balance 1), 3/2 = 1 (balance 1), 1/2 = 0 (balance 1). Este es el último paso, porque el resultado de la división es cero. Como resultado, obtuviste un número binario de 111001. Comprueba la corrección de la respuesta: 111001 = 2 ^ 0 + 2 ^ 3 + 2 ^ 4 + 2 ^ 5 = 1 + 8 + 16 + 32 = 57.
4
El segundo sistema numérico utilizado enproblemas con la computadora: hexadecimal. No son diez, sino dieciséis figuras. Para no crear nuevos símbolos, los primeros diez dígitos de hexadecimal sistemas se denotan por dígitos usuales, y los seis restantes - en letras latinas: A, B, C, D, E, F. notación decimal que corresponden número dem de 10 a 15. Para evitar confusiones, un carácter # o 0x va precedido de un número escrito en un sistema hexadecimal.
5
Para convertir un número de hexadecimal sistemas en decimal, necesita multiplicar cada uno de su número porel grado correspondiente de dieciséis y agrega los resultados. Por ejemplo, el número 11A en la notación decimal es 10 * (16 ^ 0) + 1 * (16 ^ 1) + 1 * (16 ^ 2) = 10 + 16 + 256 = 282.
6
Reverso de traducción del decimal sistemas en hexadecimal se hace por el mismo métodoresiduos, como en binario. Por ejemplo, tome el número 10,000. Al dividirlo constantemente por 16 y registrar el resto, obtendrá: 10000/16 = 625 (saldo 0) .625 / 16 = 39 (saldo 1) .39 / 16 = 2 (saldo 7) .2 / 16 = 0 (balance 2). El resultado del cálculo es el número hexadecimal # 2710. Verifique la corrección de la respuesta: # 2710 = 1 * (16 ^ 1) + 7 * (16 ^ 2) + 2 * (16 ^ 3) = 16 + 1792 + 8192 = 10000.
7
Traducir número de de hexadecimal sistemas la numeración en binario es mucho más simple. El número 16 es una potencia de dos: 16 = 2 ^ 4. Por lo tanto, cada dígito hexadecimal se puede escribir como un número binario de cuatro dígitos. Si tiene menos de cuatro caracteres en el número binario, agregue ceros al principio. Por ejemplo, # 1F7E = (0001) (1111) (0111) (1110) = 1111101111110. Compruebe la exactitud de la respuesta: ambos número de en la notación decimal es 8062.
8
Para la traducción inversa, debe dividir el binarioel número de grupos de cuatro números, comenzando desde el extremo, y cada uno de tales grupos sustituidos tsifroy.Naprimer hexadecimal, 11000110101001 convertido en (0.011) (0.001) (1.010) (1.001), que en notación hexadecimal da # 31A9. La corrección de la transferencia de respuesta confirmada en notación decimal: Tanto número de son iguales a 12713.
Consejo 5: Cómo convertir un número a binario
Debido al uso limitado de símbolos, el sistema binario es más conveniente para su uso en computadoras y otros dispositivos digitales. Los símbolos son solo dos: 1 y 0, así que esto el sistema aplicar en el trabajo de registros.

Instrucciones
1
El sistema binario es posicional,es decir. La posición de cada dígito en el número corresponde a un cierto dígito, que es igual a dos en el grado correspondiente. El grado comienza desde cero y aumenta a medida que se mueve de derecha a izquierda. Por ejemplo, número de 101 es igual a 1 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 = 5.
2
Para traducir número de desde cualquier otro sistema de numeración a binario,puede usar dos métodos: división secuencial por 2 o traduciendo cada dígito de un número en una tabla en los cuadruples correspondientes de números binarios.
3
Una amplia distribución entre los sistemas de posicióntambién usan sistemas de números octales, hexadecimales y decimales. Y si para los primeros dos, el segundo método es más aplicable, ambos son aplicables para la traducción del sistema decimal.
4
Considere la conversión de un número decimal a un número binario el sistema por un método de división sucesiva por 2. Para traducir el decimal número de 25 en código binario, necesita dividirlo por 2 parasiempre que no permanezca 0. Los residuos obtenidos en cada paso de división se escriben en la fila de derecha a izquierda, después de escribir el dígito del último resto, este será el binario final número de. Entonces: 25/2 = 12, 1 en el resto => 1; 12/2 = 6, el resto no está presente => 0; 6/2 = 3, el resto no está presente => 0; 3/2 = 1, 1 en el resto => 1; = 0, 1 en el resto => 1. El registro de la traducción es el siguiente: 25_10 = 11001_2.
5
Números octales y hexadecimalesse traducen en código binario mediante la sustitución de cada dígito que corresponde a cuatro símbolos de código del sistema binario. La tabla de traducción es la siguiente: 0 = 0,000 1 = 0001, 2 = 0,010 3 = 0011, 4 = 0,100 5 = 0101 6 = 0110 7 = 0111 = 8 1000 9 = 1,001, A = 1,010, B = 1011, C = 1100, D = 1101, E = 1110, F = 1111. Por ejemplo: 61_8 => [6 = 0110] [1 = 0001] => 01100001_2; 9EF_16 => [9 = 1001] 1110] [F = 1,111] => 100111101111_2.
Consejo 6: ¿Cuáles son los sistemas numéricos?
El sistema de números es una forma de escribir números cuandoayudar a los signos especiales, es decir, la representación del número por escrito. El sistema numérico le da al número una cierta representación estándar. Dependiendo de la época y el alcance de la aplicación, existieron y continúan existiendo muchos sistemas numéricos.

Instrucciones
1
Los sistemas numéricos existentes se pueden dividir en tres tipos principales: posicional, mixto y no posicional.
2
En los sistemas de posicionamiento, el signo o númeropuede tener un valor diferente dependiendo de la posición. El sistema está determinado por la cantidad de símbolos que se usan en él. El sistema de números decimales más popular y ampliamente utilizado. En él, todos los números están representados por una secuencia definida de diez dígitos del 0 al 9.
3
El trabajo de toda la tecnología digital se basa en un sistema de números binarios. Utiliza solo dos caracteres: 1 y 0. Todos los números grandes están representados por diferentes combinaciones de estos números.
4
En ciertos cálculos, el ternario ysistema de número octal. Conocido también es el llamado conteo por docenas o el sistema de número duodecimal. En la informática y la programación es muy popular sistema de número hexadecimal, ya que le permite grabar la palabra máquina - unidad de datos para la programación.
5
Los sistemas de números mixtos son similares a los sistemas posicionales. En sistemas mixtos, los números están representados por una secuencia creciente. La relación entre los miembros de esta secuencia puede ser completamente diferente.
6
Entonces, al sistema mixto de numeración se le puede atribuirSecuencia de Fibonacci, cada número en que es igual a la suma de los dos números previos de la secuencia, comenzando con 1. Es decir, la secuencia tiene la forma 1, 1 (1 + 0), 2 (1 + 1), 3 (1 + 2), 5 (2+ 3) y así sucesivamente.
7
Si representa un registro de tiempo en el formatodía-hora-minuto-segundo, este es también un sistema de números mixtos. Cualquiera de los términos en una secuencia se puede expresar en términos de un mínimo, es decir, en un segundo. Un ejemplo frecuentemente usado de un sistema mixto en matemáticas es el sistema de número factorial representado por una secuencia de factoriales.
8
En los sistemas de numeración sin posición, el valorsímbolo del sistema es fijo y no depende de su posición. Estos sistemas son extremadamente raros, y también son matemáticamente complejos. Ejemplos típicos de tales sistemas son: el sistema de números de Stern-Brocko, el sistema de clase residual, el sistema de números binomiales.
9
En diferentes momentos, diferentes pueblos usaronconjunto de sistemas numéricos. Por ejemplo, el sistema de numeración romano, conocido hasta hoy, era muy popular. Para escribir números, se usaron las letras latinas V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000.
10
También se conocían sistemas de numeración tales como soltero, quinario, babilónico, hebreo, alfabético, egipcio antiguo, maya, kipu e inca.







